K-means algoritmust valósítsd meg:
http://www.autonlab.org/tutorials/kmeans11.pdf
http://www.autonlab.org/tutorials/ vannak róla infók. Jó lenne a pacákat is generáltatni...
Egyebek:
megbírságolt a MÁV 6000re. (-6000)
továbbutaztam 1 megállóval a menetjegyemen feltüntetettnél (+140)
egyik úton egyáltalán nem fizettem (+940)
SUM: -4920
... eddig!
~~~
A következő címkéjű bejegyzések mutatása: suli. Összes bejegyzés megjelenítése
A következő címkéjű bejegyzések mutatása: suli. Összes bejegyzés megjelenítése
2009/12/03
2009/11/19
IAR ea
mozgásérzékelés webkamerával TODO in ColorHead:
http://archiv.mee.hu/elletoltes/2005/2005_10/mozgaserzekeleswebkameraval.pdf
Lépések amúgy:
~~~
http://archiv.mee.hu/elletoltes/2005/2005_10/mozgaserzekeleswebkameraval.pdf
Lépések amúgy:
- simítás
- különbséget veszünk
- esetleg simítunk megint
- különbséget maszkként használva eltérés vizsgálat
~~~
2009/11/18
2009/10/08
splineok megint
Spline
1- sarokpontok helyzetére yi-1=fii(xi-1); yi=fii(xi)
2- fi’(xi)=fii+1’(xi)
3- yi’’(xi)= fii+1’’(xi)=mi
fii(x)=-mi-1*(x-xi)^3/6*hi+mi*(x-xi-1)^3/6*hi+((yi-yi-1)/hi-mi-mi-1)*hi/6*x +((yixi-1+yi-1*xi)/hi)
Ha egy mátrixban a főátlóban lévő elemek dominálnak, akkor megoldható.
http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf
~~~
2009/10/01
Egy kicsi az általános spline-okról
Spline:
sarokpontjaink (xi,yi) i=0,1,...n
(1)

(2)
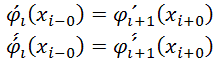
n db 4-adfokú 4n paraméter lesz
hi = xi-xi-1
fi''i(xi) = mi
fi''i(xi-1) = mi-1
---
fi''i(x) = -mi-1*(x-xi)/(xi-xi-1)+mi*(x-xi-1)/(xi-xi-1)
fi'i(x) = -mi-1*(x-xi)^2/(2*hi)+mi*(x-xi-1)^2/(2*hi)+c1i
fi(x) = -mi-1*(x-xi)^3/(6*hi)+mi*(x-xi-1)^3/(6*hi)+c1i*x+c2i
1(a) feltételbe behelyettesítünk
yi-1=-mi-1*hi^2/6+c1i*xi-1+c2i
1(b) feltételbe is:
yi = mi*hi^2/6+c1i*xi+c2i
ezután yi-yi-1 =mi*hi^2/6+mi-1*hi^2/6+c1i*(xi-xi-1) --> c1i = (yi-yi-1)/hi - (mi+mi-1)*hi/6
yi*xi-1-yi-1*xi = mi*hi^2/6*xi-1 + c2i*xi-1+mi-1*hi^2/6*xi-c2i*xi
--> c2i = (mi*xi-1+mi-1*xi)*hi/6-(yi*xi-1-yi-1*xi)/hi
OMG.
ezután mi-t fejezzük ki, és az agyunkat elfolyatjuk.
köszönöm a figyelmet.:-)
sarokpontjaink (xi,yi) i=0,1,...n
- feltételezzük, hogy 2szer folytonosan deriválható fv.-ből származik az yi
- x szerint rendezve vannak.
- harmadfokú polinomokkal közelítünk
- sima áthaladás legyen a sarokpontokon
- az 1. és a 2. deriváltra is legyen feltevésünk, de nem fix értékekként
- sarokpontoknál ne legyen hirtelen változás
(1)

(2)
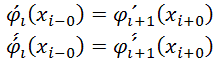
n db 4-adfokú 4n paraméter lesz
hi = xi-xi-1
fi''i(xi) = mi
fi''i(xi-1) = mi-1
---
fi''i(x) = -mi-1*(x-xi)/(xi-xi-1)+mi*(x-xi-1)/(xi-xi-1)
fi'i(x) = -mi-1*(x-xi)^2/(2*hi)+mi*(x-xi-1)^2/(2*hi)+c1i
fi(x) = -mi-1*(x-xi)^3/(6*hi)+mi*(x-xi-1)^3/(6*hi)+c1i*x+c2i
1(a) feltételbe behelyettesítünk
yi-1=-mi-1*hi^2/6+c1i*xi-1+c2i
1(b) feltételbe is:
yi = mi*hi^2/6+c1i*xi+c2i
ezután yi-yi-1 =mi*hi^2/6+mi-1*hi^2/6+c1i*(xi-xi-1) --> c1i = (yi-yi-1)/hi - (mi+mi-1)*hi/6
yi*xi-1-yi-1*xi = mi*hi^2/6*xi-1 + c2i*xi-1+mi-1*hi^2/6*xi-c2i*xi
--> c2i = (mi*xi-1+mi-1*xi)*hi/6-(yi*xi-1-yi-1*xi)/hi
OMG.
ezután mi-t fejezzük ki, és az agyunkat elfolyatjuk.
köszönöm a figyelmet.:-)
2009/09/24
IAR 3. ea
Ízületi mozgásra feltételek
a) megengedett tűréssel a sarokpontokat (durva pályatervezésből) el kell érni
b) végpontokban a sebesség, és a gyorsulás is 0
c) izületi sebesség, és gyorsulás folytonos fv. szerint változik
d) izületi seb. és gyorsulás értékek egy jellemző határértéket nem léphetnek át.
qj = izület
˙qj = sebesség
¨qj = gyorsulás
Lineáris pályatervezés parabolikus átmenettel
Elv:


gyorsulás = 0 a Ti-tau és Ti+tau helyeken



így már ki lehet fejezni az izületet, a sebességet és a gyorsulást a t függvényében. (ezt hosszúság miatt nem írom le, csak be kell helyettesíteni.)
Tranziens idő meghatározása(τB)
¨qjmax:
a) maximuma: (hárompöttyös:) ¨˙q(t)=2kt=0 --> t=0
τB = 3/4 * (v1-v0)/¨qjmax
És most szünet :)
a) megengedett tűréssel a sarokpontokat (durva pályatervezésből) el kell érni
b) végpontokban a sebesség, és a gyorsulás is 0
c) izületi sebesség, és gyorsulás folytonos fv. szerint változik
d) izületi seb. és gyorsulás értékek egy jellemző határértéket nem léphetnek át.
| x | magyarázat | pozíció | sebesség | gyorsulás |
| x0 | első pozíció | 0 | 0 | |
| xi | közbenső pozíció | qjmin<=qji<=qjmax és |qji-q*ji|<--ε | ˙qji- = ˙qji+ és |qji|<|qjmax| | ¨qji- = ¨qji+ és |qji|<|qjmax| |
| xf | végső | 0 | 0 |
qj = izület
˙qj = sebesség
¨qj = gyorsulás
Lineáris pályatervezés parabolikus átmenettel
Elv:
- szakaszonként lineáris az összekötésű
- 2τ átmeneti idő: beérkező seb => kiindulási seb. τ-t maximális ízületi gyorsulás határozza meg


gyorsulás = 0 a Ti-tau és Ti+tau helyeken



így már ki lehet fejezni az izületet, a sebességet és a gyorsulást a t függvényében. (ezt hosszúság miatt nem írom le, csak be kell helyettesíteni.)
Tranziens idő meghatározása(τB)
¨qjmax:
a) maximuma: (hárompöttyös:) ¨˙q(t)=2kt=0 --> t=0
τB = 3/4 * (v1-v0)/¨qjmax
És most szünet :)
Feliratkozás:
Bejegyzések (Atom)
