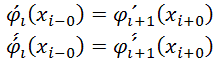splineok megint

Spline

1- sarokpontok helyzetére yi-1=fii(xi-1); yi=fii(xi)

2- fi’(xi)=fii+1’(xi)

3- yi’’(xi)= fii+1’’(xi)=mi

fii(x)=-mi-1*(x-xi)^3/6*hi+mi*(x-xi-1)^3/6*hi+((yi-yi-1)/hi-mi-mi-1)*hi/6*x +((yixi-1+yi-1*xi)/hi)
hi*mi-1+2(hi+hi+1)mi+hi+1*mi+1=6*((yi+1-yi)/(hi+1)-(yi-yi-1)/(hi+1))

Ha egy mátrixban a főátlóban lévő elemek dominálnak, akkor megoldható.

http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf

~~~

Egy kicsi az általános spline-okról

Spline:
sarokpontjaink (xi,yi) i=0,1,...n

• feltételezzük, hogy 2szer folytonosan deriválható fv.-ből származik az yi
• x szerint rendezve vannak.
• harmadfokú polinomokkal közelítünk
• sima áthaladás legyen a sarokpontokon
• az 1. és a 2. deriváltra is legyen feltevésünk, de nem fix értékekként
• sarokpontoknál ne legyen hirtelen változás
  

feltételek:
(1)






(2)





n db 4-adfokú 4n paraméter lesz
hi = xi-xi-1
fi''i(xi) = mi
fi''i(xi-1) = mi-1
---
fi''i(x) = -mi-1*(x-xi)/(xi-xi-1)+mi*(x-xi-1)/(xi-xi-1)
fi'i(x) = -mi-1*(x-xi)^2/(2*hi)+mi*(x-xi-1)^2/(2*hi)+c1i
fi(x) = -mi-1*(x-xi)^3/(6*hi)+mi*(x-xi-1)^3/(6*hi)+c1i*x+c2i

1(a) feltételbe behelyettesítünk
yi-1=-mi-1*hi^2/6+c1i*xi-1+c2i
1(b) feltételbe is:
yi = mi*hi^2/6+c1i*xi+c2i

ezután yi-yi-1 =mi*hi^2/6+mi-1*hi^2/6+c1i*(xi-xi-1) --> c1i = (yi-yi-1)/hi - (mi+mi-1)*hi/6
yi*xi-1-yi-1*xi = mi*hi^2/6*xi-1 + c2i*xi-1+mi-1*hi^2/6*xi-c2i*xi
--> c2i = (mi*xi-1+mi-1*xi)*hi/6-(yi*xi-1-yi-1*xi)/hi
OMG.
ezután mi-t fejezzük ki, és az agyunkat elfolyatjuk.

köszönöm a figyelmet.:-)